The Choice of Discount Curve
Despite what textbooks on the pricing of corporate bonds might claim, in our previous blog post, we established what interest rate derivatives discounting is not – it’s nothing to do with adjusting for counterparty risk.
The value today of a future, possibly risky, cashflow CT is correctly computed as the credit-adjusted expectation value of the cashflow, appropriately discounted:
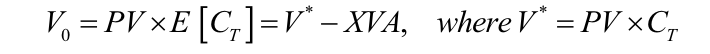
- V* represents the value in a default-free idealised world – so the cashflow is from e.g. an exchange.
- The calculation of the XVA adjustments is a subject for another day.
Now that we have correctly divorced discounting from the issue of pricing default risk, we can address the issue of what the PV factor in the formula above is. What rate should discounting be at?
The answer is that we should discount at our own cost of funding.
Here’s why: imagine a bank purchases an exchange-traded instrument that promises a future cashflow VT, for the fair market price V0. This is, by definition, a PV=0 trade.
The cashflows on the deal, inclusive of the bank’s funding, look like this:

If this trade is PV = 0 (which it is), then the cashflows at t = T must net to zero, and therefore
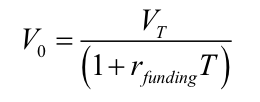
- Or, in words, your discount rate is your funding cost.
At face value, this is a rather disturbing result: it says that there is no such thing as a unique fair market price since there is no unique funding cost that applies to all market players. (We note in passing that the pre-2008 practice of discounting at LIBOR neatly solved this problem, by pretending that LIBOR was a universal proxy for the funding cost of all banks.)
If there isn’t a unique fair price for a derivative, the consequences are profound:
- No concept of fair mark-to-market

- Bilateral – and therefore logically zero-sum – derivative contracts are no longer zero-sum all sorts of paradoxes

- Liquidity dries up in the interbank market, as participants cannot agree on where mid-market is and are therefore reluctant to trade

- Prices worsen and liquidity dries up for the buy-side, as sell-side banks suffer from an inability to hedge in the interbank market
This vicious cycle represents an existential threat to the derivatives market. Luckily, CSAs – and central clearing – come to the rescue.
Collateral and OIS Discounting
The widespread adoption of CSAs in the OTC world to match margining in the exchange-traded (or centrally-cleared) world, was a response to the global crisis of 2008-2009 – widely (if not entirely accurately) seen as a credit crisis.
But collateral does something else; it addresses both the issue of counterparty risk and the issue of derivatives funding.
To understand why consider a simple toy transaction: bank A buys a derivative, for instance, a call option, from a customer for a premium P. The call option has an expected payoff (according to Black-Scholes) of VT.
With no CSA in place, the deal looks like this:

- And the trade is marked in the bank’s books at , i.e. discounted at the bank’s wholesale cost of funds (LIBOR ++, for most), a number that is different for every bank.
With a CSA in place, the picture is different:
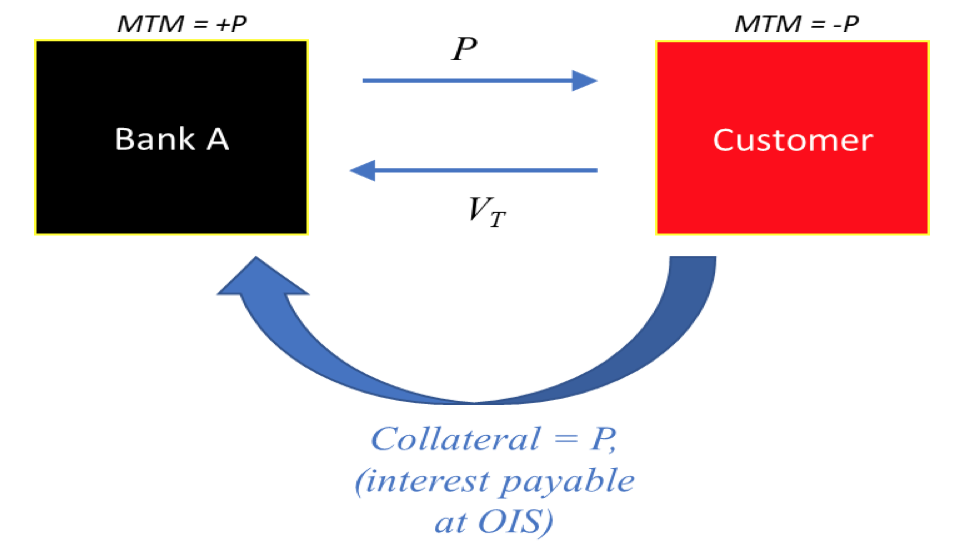
Now there is no external wholesale funding required because the premium is auto-funded by the transfer of collateral. And therefore, the effective cost of funding is the interest payable on the collateral account, which is OIS, and so OIS is the right curve for discounting.
A Few Points are Worth Emphasising
This argument, that any funding/reinvestment requirements will be covered by collateral transfers, doesn’t just hold for option premiums as above but is generally true for any derivatives position on a risk-neutral expectation value basis.
If you need to convince yourself that this is true, just think about how the market defines/computes a forward price.
– The argument above does not just hold at trade level – collateral is computed on a netted portfolio basis, so OIS discounting applies to all instruments within the portfolio governed by the same CSA
– We have (almost) solved the ‘uniqueness’ problem we previously discussed – because all CSAs are (at least to first-order) the same; they all specify that interest is payable at the market’s ‘official’ overnight RFR
– And even when the CSA has anomalous terms such as zero-strike EURIBOR floors, it is convenient to use the same formalism and deal with the anomalies as standalone adjustments (another XVA)
Summary and Conclusions
‘Standard’ CSAs (ISDA’s ‘SCSA’) specify interest is payable on posted cash collateral at OIS, and therefore that is the right curve to use for valuing a cash-collateralised derivatives portfolio. This is what has naturally become known as ‘OIS discounting’.
The calculation of the OIS discount curve – i.e. DF(t) – from the par OIS curve is a straightforward calibration exercise, popularly known as ‘bootstrapping’. I imagine this is familiar to most readers, but if not, you should come to the next running of LFS’s Interest Rate Derivatives and Swaps, where we do lots of bootstrapping.
This is all good, but problems remain.
What if:
- The CSA allows collateral to be posted in cash, but in another currency?
- The CSA allows collateral to be posted in the right currency, but in government bonds?
- Or even worse, the CSA allows multiple choices of the collateral format?
In part three of this series, we will address these questions and establish what is meant by ‘CSA discounting’.
Related Courses
Interest Rate Derivatives and SwapsInterest Rate Derivatives 2: Options
Interest Rate Derivatives 3: Structuring
