Modern Derivatives Pricing – CSA Discounting

When Collateral is Posted in the ‘Wrong’ Currency

In our previous blog on Modern Derivatives Pricing we established two important facts which underpin pricing:

• The discount curve should reflect the cost of funding – not counterparty credit
• In an ideal world – central clearing; or perfect CSAs in an OTC context – all funding requirements are met by transfer of collateral

As a result, if the CSA specifies that collateral be posted in the same currency as the underlying position which needs the funding, then the discount rate should be the rate one pays on posted collateral, which is OIS.

This was the basis of the OIS revolution of 2008 when the derivatives community switched, in some cases reluctantly – there were still diehard LIBOR-discounters as late as 2011 – to OIS discounting for their derivatives books.

But what if the CSA allows the posting of collateral in a different currency (USD is common)? As a concrete example, let’s consider a EUR-denominated derivative position over 24-hours, roughly, CoB on day one to CoB on day two.

If the position is collateralised with EUR cash, the timeline of cashflows looks like this:

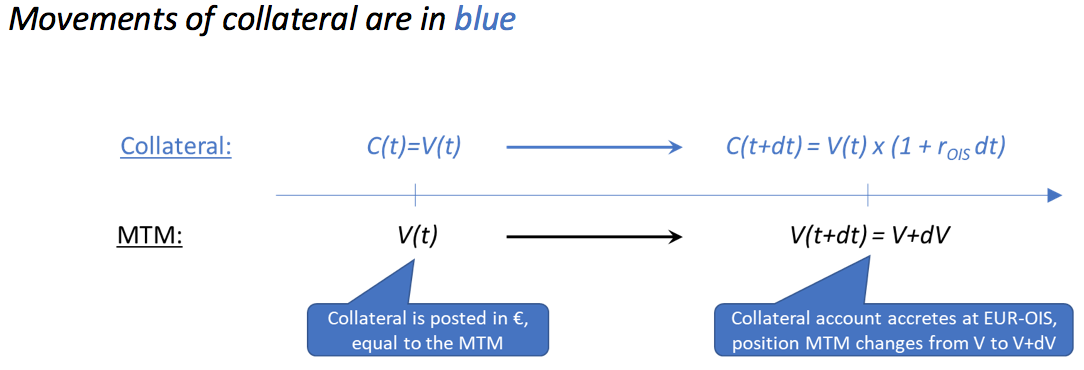
If the collateral account is to exactly match the MTM of the position, we require C(t+dt) = V(t+dt) and therefore . This has the obvious solution

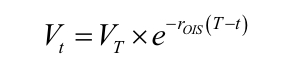
Which just confirms what we had already concluded, that derivatives are correctly discounted at OIS.

Cross-currency Swaps

Now, we consider the case where collateral is posted in USD. Since the collateral must be available in EUR to do its required job of funding the position, the collateral needs to be converted into USD every day. This is achieved by an overnight FX swap:                                                               

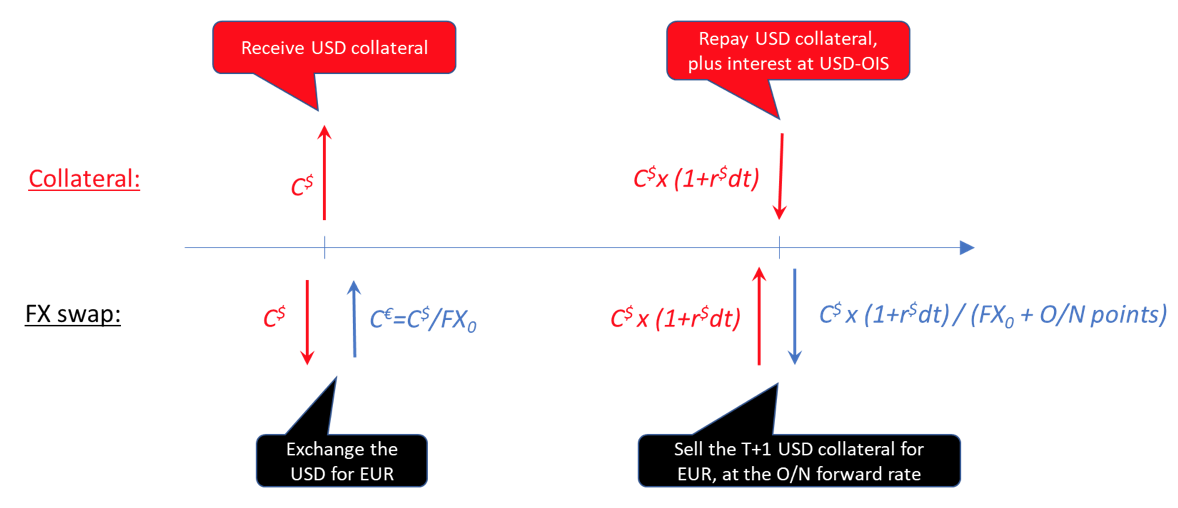
Netted with the cashflows on the FX swap, all the USD cashflows disappear and we have achieved EUR funding for our EUR position. But at what all-in cost?

From the FX rate we will trade at on the far leg – the bid-side of the EUR USD O/N forward points – we can calculate an effective cost of funding in EUR, as follows:

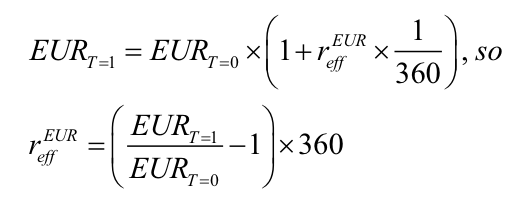
This is the adjusted rate – extrapolated to all maturities to get a proper term-structure – that we must use to discount our EUR-denominated position.

It is standard practice to write , and in a slightly roundabout fashion, we have now arrived at something that looks like the cross-currency basis you are probably familiar with from the swaps world. And it almost is, except that the CRX basis which actually trades is (for now, at any rate) the 3M-LIBOR / 3M-EURIBOR basis; but what we have arrived at is the OIS/OIS basis spread. Numerically, this will be smaller since most of the IBOR/IBOR basis is down to the respective LOIS spreads in the two currencies, and we have stripped that out.

(Cheeky advertisement! It helps to have a good understanding of the mechanics and pricing of cross-currency swaps. Sign up to the next running of our Interest Rate Derivatives and Swaps if you feel you would benefit from a more in-depth discussion.)

This is a little tricky and messy; an example might help to make it clear.

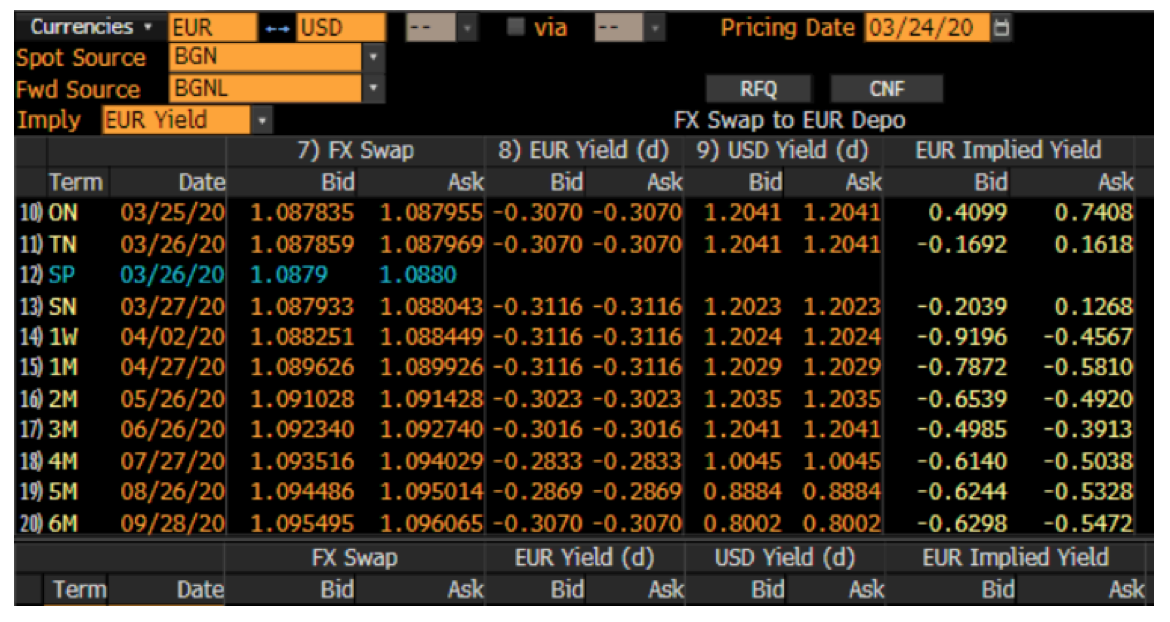
Suppose we want a 6M EUR discount factor. If the position is collateralised with EUR cash, then we use the EUR-OIS rate of -0.307% and the answer is; 6 months = 186 days

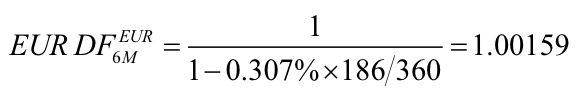
If the position is collateralised with USD, we can do a simple calculation – a generalised version of the one in formula 1.2 – to extract the implied EUR rate from the quoted forward points (+76). From the classic no-arb forward FX formula, with a 6M USD OIS rate of 0.8002%, we know that

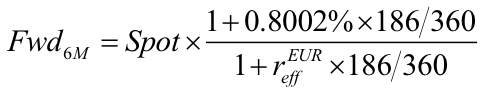
With Spot = 1.0879, and 6M = 1.095495, we get a rate of -0.5472%, in agreement with Bloomberg (right-hand column), which corresponds to a CRX basis of -23 bp.

The 6M discount factor in this case is 1.00284.

When Collateral is Posted in Government Bonds

Although cash is optimal, it is common to post collateral in the form of government bonds and some asset managers and pension funds’ CSAs demand it. The analysis is very similar to what we just did on posting collateral in currency.

Suppose we have a USD-denominated derivatives position, and the other side is posting collateral in USTs. Again, we have to convert the USTs into cash on a daily basis, and the mechanism for doing so is the repo market:

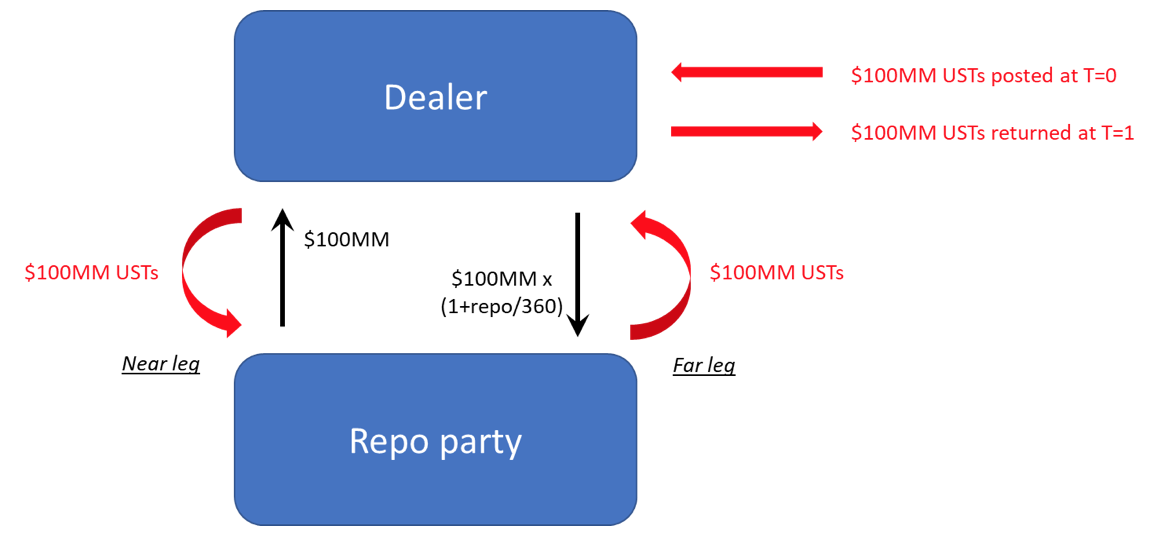
As the diagram shows, reverse-repoing the posted Treasuries generates cash at a cost of overnight repo. The (offered-side of) the market repo rate is therefore the correct curve to use for discounting this position.

A couple of observations

• Since the OIS rate in USD is SOFR, which is a median of repo rates, the adjustment for USD will be tiny (as of March 15^th 2021, both SOFR and O/N repo are trading at 0.01%).
• The long-end of the repo curve is just the Treasury curve, so UST-collateralised positions are discounted at Treasuries, which makes sense
• In other currencies there is a clear distinction between OIS rates and repo rates, so the effect on the discount curve will be more noticeable. In particular, both SONIA (UK) and €STR (Eurozone) are unsecured rates and should trade above GC repo.

The CTD Delivery Option

The final situation to be discussed is the case where the CSA allows choices. For example, the party posting collateral has a choice between domestic cash / USD; or domestic cash / domestic Govies.

The assumption that a dealer must make is that their counterparty will act rationally, and post collateral in the format that is best for them and therefore worst for us; in this case ‘best for them’ means highest-yielding and so most expensive, from our perspective. This optionality is referred to as the ‘CTD option’ in collateral posting – note that it has nothing to do with the phrase CTD in connection with bond futures.

So when we construct our discount curve the rate at each node in the bootstrap algorithm will be, at a minimum

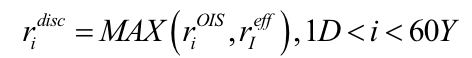
In reality it will be worse, since 1.3 only captures the intrinsic value of the CTD option. In reality, the input rates to the discount curve really will be

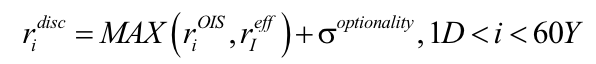
A discussion of the computation of the value of the CTD option ­– a very hard problem – is beyond the scope of this introductory note.

Related Courses